Improving NNs

2023-01-21

4 minute read

Notes , Mathematics , ML , NNs

Measurements of fit

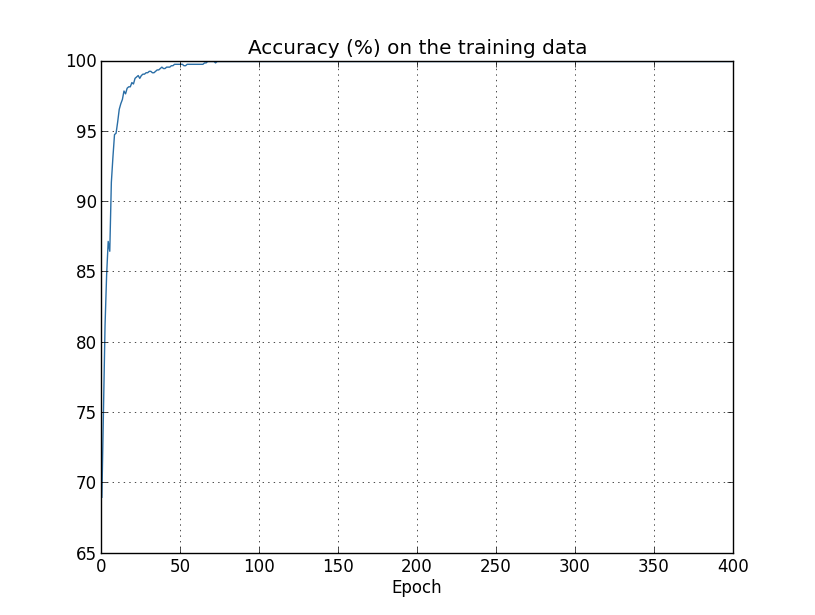
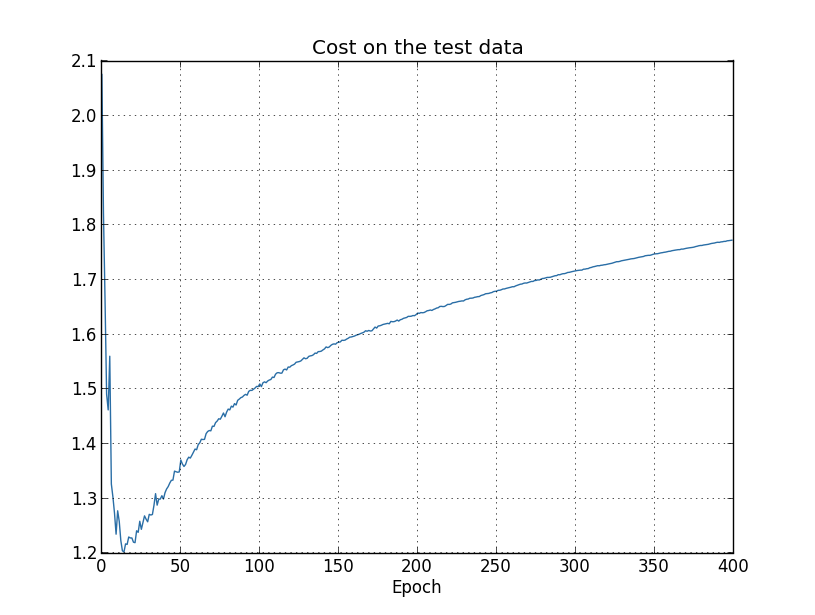
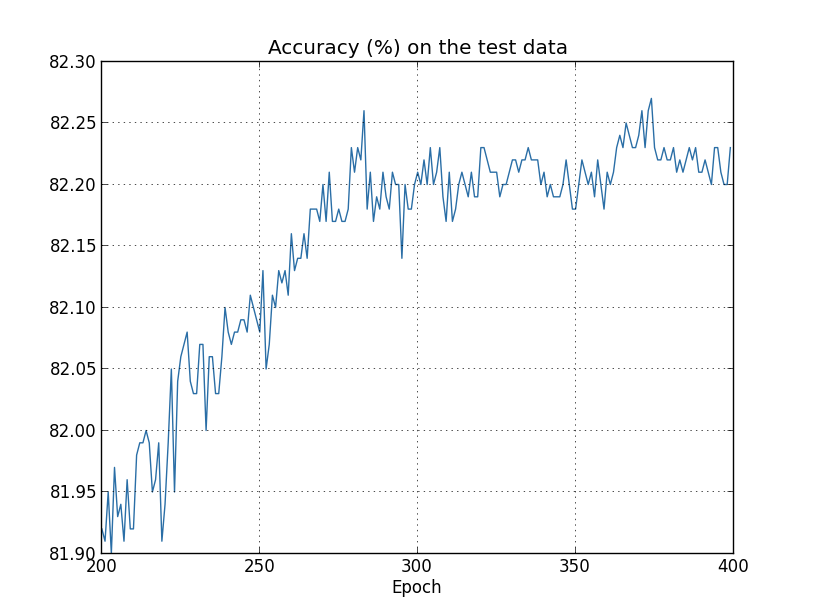
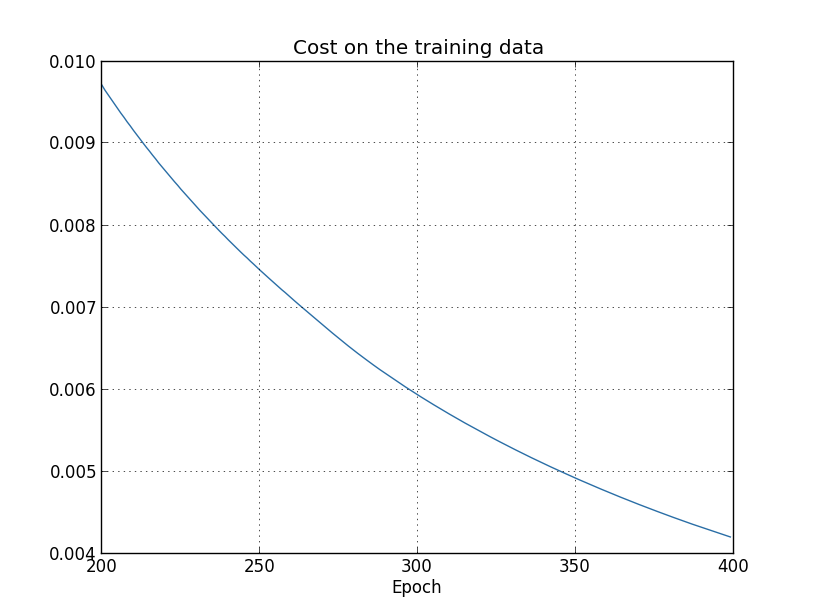
From Neural Networks and Deep Learning, 4 measures of the same data to check how good the fit is:

Here accuracy on the test data plateaus around epoch 280, while the training data cost keeps going down smoothly. On the other hand, the cost for the test data starts going up around epoch 15, which is more or less the same point that the accuracy on the training data stops drastically improving. It looks like it memorized the training data around epoch 280.
The network starts overfitting around epoch 280, which simply means that it’s not generalizing anymore
The cost function is a proxy for the overall accuracy, so the test data accuracy is more important than the test data cost - hence epoch 280, rather than 15
The difference between training and test accuracy is ~18%. This is Bad, and another sign of overfitting
One of the best ways to avoid overfitting is to increase the amount of training data. Hehe
If the model doesn’t overfit on a small subset of the data, it probably won’t fit properly on a larger set? Makes sense, but might not be true

Early stopping is training until the classification accuracy for the validation set stops improving
Early stopping can be too soon, as sometime the accuracy takes a break and then starts improving again (something to do with grokking?)
Training data is used to check whether the parameters are getting properly trained, validation data to check whether the hyperparameters are correct
The hold out method is keeping the validation data apart from the test data, in order to find good hyperparameters

Techniques that are used to calibrate machine learning models in order to minimize the adjusted loss function and prevent overfitting or underfitting

Works by adding an extra cost based on the weights of the NN
Basically amounts to $C = C_0 + \lambda R$, where $C_0$ is the base cost function (e.g. cross-entropy), $\lambda$ is a scaling factor called the regularization term, and $R$ is the actual regularization function

Encourages the weights to stay small
Regularization doesn’t include the biases - only the weights
$\frac {\partial C}{\partial w} = \frac {\partial C_0}{\partial w} + \frac {\lambda}{n}w$, which is nice and simple to calculate
The weight update is $w = \begin{pmatrix} 1 - \frac {\eta \lambda}{n} \end{pmatrix}w - \eta \frac {\partial C_0}{\partial w}$. This will cause all weights to be scaled down, unless they are actively contributing to the network?
Regularizing the biases doesn’t seem to give too much, empirically. One the other hand, allowing large biases give more flexibility

Won’t penalize outliers as much as L2 does
The weight update is $w = w - \frac {\eta \lambda}{n} \text{sign}(w) - \eta \frac {\partial C_0}{\partial w}$ (where $\text{sign}(x)$ is the sign of x). This will always shrink the weights towards 0 by a constant, as opposed to L2 where it shrunk them by an amount proportional to $w$
L1 will concentrate the weights in a small number of high importance connections, shrinking the rest to 0
Would this mean that weights don’t go to 0, just jump around it?

Works by temporarily removing a portion of neurons from the hidden layer for each batch
The fraction is e.g. half of the neurons
Input and output layers can’t be removed, as that would change the function signature
Intuitively, this amounts to training a large amount of smaller networks and averaging their outputs
The learned weights need to be scaled down, as (for $p=0.5$) they will be twice as large as they should be
Especially useful in large, deep networks
The network learns to manage even if some of its inputs are missing

More data $\to$ better learning, but getting data is hard
Slightly rotating, expanding etc. images doesn’t make them less recognizable $\to$ adding random perpetuations to the training data will generate a lot of new but valid data
The data set is crucial - an outstanding, magnificent algorithm might turn out to simply be good at a given data set and be rubbish on other data

A basic idea is Gaussian with mean 0 and std dev 1
a std dev of 1, with a lot of parameters will result in the overall std dev of $z$ to be quite large. Which in turn will saturate $\sigma$ activation functions. A much better idea is to initialize with a std dev of $\frac 1 {\sqrt {n_{in}}}$, which will result in the initial std dev of $z$ being around 1
Using $\frac 1 {\sqrt {n_{in}}}$ will result in the network start off a lot faster, but can also sometimes make the final result better